
1.1.1 실리콘 결정 구조
실리콘(Silicon, Si)은 반도체 소자에서 흔히 사용되는 물질입니다. 반도체는 전도체와 부도체로 나뉘며, 실리콘은 에너지 밴드(Energy Band)에서 적절한 밴드 갭(Band Gap)을 가지고 있어 도체와 부도체로 조절할 수 있는 특징을 갖추고 있습니다.
이를 위해서는 원자의 최외곽 전자가 4개여야 합니다. 실리콘뿐만 아니라 게르마늄(Ge), 화합물인 갈리움비소(GaAs) 등도 해당합니다. 그러나 실리콘은 모래로부터 생산하기도 용이하여 저렴하게 구할 수 있어 대표적으로 사용됩니다. 또한, SiO2와 같이 우수하고 쉽게 만들 수 있는 산화막을 형성할 수 있습니다.
실리콘은 다이아몬드 구조를 가지며, 결정 구조는 Si이 서로 엉겨 붙어 3차원 구조를 형성합니다. 이때의 주기적인 구조의 기본 단위를 Unit Cell이라 하며, 해당 단위의 길이는 5.24Å입니다. (1Å = 10^(-10) m)
1.1.2 방향성을 나타내는 Miller Index
결정 구조의 방향을 나타내기 위해서는 Miller Index가 사용됩니다. (abc) 안에 있는 숫자가 Miller Index이고, (###)은 면을, [###]은 면에 수직 한 결정 방향을 나타냅니다.
여기서 a, b, c의 값은 각각 1/a, 1/b, 1/c와 x, y, z 축과 교차하는 값을 의미합니다. (100)은 x축과 1번 교차하며 y, z 축과는 무한대로 교차하지 않는 면을 나타냅니다. 반면에 (111)은 x, y, z 축과 각각 1번 교차하는 면입니다.
이러한 방향성은 특히 Miller Index를 통해 구분되며, 일반적으로 '일빵빵' 또는 '일일빵'과 같이 표현됩니다. 주로 일빵빵을 사용하긴 하지만 특정 특성에 따라 다른 면도 사용되곤 합니다.

1.2.1 전자와 정공의 결합 모델
Si 원자는 주변에 4개의 근접한 이웃 Si 원자들로 둘러싸여 있습니다. Si의 최외각 전자 중 하나는 이웃한 Si 최외곽 전자와 공유 결합을 형성합니다. 이 구조가 계속 반복되면 남는 전자, 즉 자유 전자가 없다는 가정하에도, 상온에서는 열 에너지의 영향으로 공유 전자 일부가 자유 전자가 될 수 있습니다.
자유 전자가 격자 사이에서 자유롭게 이동하면 전도가 발생하여 전류를 운반할 수 있습니다. 격자에서 벗어난 전자가 남으면 빈자리가 생기는데, 이를 정공(Hole)이라고 부릅니다. 자유 전자는 격자 사이로 움직이거나 빈 공간으로 움직일 수 있습니다. 이를 빈 공간의 구멍이 이동하는 것으로 생각하면, Hole은 양의 전하를 가진 전자와 같은 Carrier로 간주됩니다.
한 개의 공유 결합된 전자를 자유롭게 만들기 위해서는 1.1eV의 에너지가 필요합니다.
1.2.2 도너와 억셉터 (Donor and Acceptor)
상온에서는 전자와 정공의 농도가 상대적으로 적습니다. 상온에서 캐리어(전자, 정공)를 더 많이 만들기 위해 불순물을 도핑(Doping)하여 넣습니다. 도핑에 사용되는 물질에 따라 전자나 정공의 양이 증가합니다.
As(Arsenic)은 최외각 전자가 5개인 원소로, Si보다 하나 더 많은 전자를 가지고 있습니다.As 도핑을 하면 자유 전자가 추가로 생기며, 이는 Si 원자의 자리에 As가 들어가서 주변 Si 최외곽 전자와 공유 결합을 형성하고 남은 전자가 높은 농도의 자유 전자가 됩니다. 전자를 제공하는 As를 Donor라고 하며, Majority Carrier는 전자, Minority Carrier는 정공이 되어 N type 반도체로 분류됩니다.
Si보다 하나 적은 최외각 전자를 가진 B(Boron)을 도핑하면 Hole이 추가로 발생합니다. B를 Acceptor라고 하며, Hole이 Majority Carrier가 되어 P type 반도체로 분류됩니다. As 도핑을 하면 이온화 에너지는 1.1eV에서 50 meV로 줄어들어 상온에서 Carrier 농도가 증가합니다.

1.3.1 에너지 밴드
Si 결정 내에서 최외곽 전자들은 동일한 에너지 준위에 존재할 수 없습니다. 이는 파울리 베타 법칙에 기인합니다. 파울리의 베타 법칙은 두 개 이상의 전자가 동일한 상태를 공유할 수 없다는 원리를 나타냅니다.
Si 결정 내에서 Si 원자가 많이 근접하게 위치하고 있기 때문에 많은 전자들도 서로 근접하게 되며, 동일한 에너지 준위에서 공존할 수 없는 상태들이 모여 밴드 형태로 형성됩니다. 이 Band의 가운데를 Band Gap, 위 쪽 Band를 Conduction Band, 아래쪽 Band를 Valence Band로 지칭합니다. Valence Band에는 절대 온도 기준으로 전자가 가득 차 있으며, 전류가 흐르려면 Valence Band의 전자들이 Conduction Band로 이동해야 합니다. Band Gap의 크기에 따라 전류의 흐름이 결정되며, 이 값이 작을수록 전류 흐름이 쉽고, 클수록 어려워집니다.
Si의 Energy Band Gap은 1.1eV이며, 최외곽 전자가 격자를 벗어나 자유 전자가 되기 위한 이온화 에너지는 1.1eV입니다.
SiO2는 9.0eV, SiN은 5.5eV의 Energy Band Gap을 가집니다. 도핑을 통해 이온화 에너지가 감소하면, Donor Energy Level (Ed)과 Acceptor Energy Level (Ea)이 생깁니다. 도핑을 통해 Ed와 Ea의 값이 각각 Ec와 Ev의 차이보다 작아지면, Carrier(전자, 정공)의 이온화가 더 쉬워지게 됩니다. 이로써 Si 결정 내에서의 Carrier 생성 및 전류 흐름이 상온에서도 활발히 일어나게 됩니다.


1.4.1 도체, 반도체, 절연체 (Conductor, Semiconductor, Insulator)
EBD(Energy Band Diagram)를 활용하여 반도체, 절연체, 그리고 도체의 차이점을 살펴볼 수 있습니다.
Eg는 Conduction Band (Ec)와 Valence Band (Ev)를 분리하는 에너지를 나타냅니다.
- 절연체(Insulator):
- Eg가 매우 크기 때문에 Valence Band의 전자들이 Conduction Band로 이동하기 어렵습니다.
- 전류 전도에 기여하지 않습니다.
- 보통 4eV 이상의 큰 Eg를 가지며, 다이아몬드와 같이 6eV 이상인 물질도 절연체 특성을 보일 수 있습니다.
- 반도체(Semiconductor):
- Eg가 적당히 작아서 적당한 에너지가 가해지면 전자가 Conduction Band로 이동하여 전류 전도에 기여할 수 있습니다.
- Eg의 크기에 따라서도체나 절연체의 특성을 나타냅니다.
- 도체(Conductor):
- Eg가 아주 작고, Conduction Band에 전자가 어느 정도 채워져 있는 경우입니다.
- 외부 에너지의 가해 없이도 전류가 자유롭게 흐릅니다.
이러한 특성에 따라 반도체는 Eg의 크기에 따라 도체로도, 절연체로도 동작할 수 있는 유연성을 갖고 있습니다

1.5.1 전자 및 정공
전자(electron)는 대부분 Valence Band에 위치한 전자들 중에서 발생합니다. 전자는 Valence Band에서 Conduction Band로 전이하여 전류를 생성하는데 사용됩니다. 이는 전자를 Valence Band에 있던 전자가 아닌, 전도가 가능한 전자로 가정한다는 것을 의미합니다.
정공(hole)은 Valence Band에 있는 전자의 결여된 상태입니다. 전자가 Valence Band를 떠나면 해당 위치에는 정공이 생성되며, 정공은 양전하를 가진 입자로서 전자의 반대로 +q 전하를 운반합니다.
EBD(Energy Band Diagram)에서 높은 위치는 전자의 높은 에너지를 나타냅니다. 전도되는 전자의 최소 에너지는 Conduction Band의 최소 에너지(Ec)이며, Ec보다 큰 모든 에너지는 전자의 운동 에너지로 간주됩니다. 이 운동 에너지는 전자가 전기장 내에서 가속되고 결정 내 격자나 결함들과 충돌하면서 에너지를 소모합니다. 정공의 위치가 낮을수록 에너지가 높아지며, Valence Band의 최소 에너지는 Ev입니다.
1.5.2 유효 질량
전자와 정공의 운동을 묘사하기 위해서는 유효 질량(effective mass)를 이해해야 합니다. 결정 내에 있는 전자들은 주변 전하에 의해 영향을 받기 때문에 자유 전자 질량과는 다를 수 있습니다. 유효 질량을 구하는 방법으로는 슈뢰딩거 파동 방정식을 활용하거나 Cyclotron resonance 기법을 통해 실험 값을 얻을 수 있습니다. 이러한 실측 및 계산된 유효질량은 특정한 물질에 대한 Table을 참고하여 확인할 수 있습니다.
| Effective mass | Si | Ge | GaAs | InAs | AlAs |
| mn/m0 | 0.26 | 0.12 | 0.068 | 0.023 | 2 |
| mp/m0 | 0.39 | 0.3 | 0.5 | 0.3 | 0.3 |
1.6.1 상태 밀도
상태 밀도(Density of State)는 전자와 정공의 농도를 계산하기 위한 중요한 개념입니다. 전자는 불확실성의 원리로 인해 에너지와 위치를 동시에 정확히 알 수 없으므로, 확률적인 계산을 통해 전자의 농도를 파악합니다. 모든 가능한 상태의 확률을 곱하면 원하는 경우의 수가 나오는 것처럼, 전자가 존재할 수 있는 모든 에너지 상태의 확률을 곱하여 농도를 구할 수 있습니다.
한 상태는 파울리 베타 법칙에 따라 전자가 그 상태에 있거나 없거나 둘 중 하나입니다. 상태 밀도를 계산하는 방법은 주어진 에너지 범위 내의 상태 수를 해당 에너지와 부피로 나누는 것입니다.
Conduction Band의 상태 밀도(Dc)와 Valence Band의 상태 밀도(Dv)가 있습니다. Dc와 Dv는 각각 (E-Ec)^(1/2) 및 (Ev-E)^(1/2)에 비례하며, 이는 상태 밀도를 정의하는 데 사용됩니다.
상태 밀도를 통해 물질 내에서 전자와 정공의 확률적인 위치와 에너지에 대한 정보를 얻을 수 있습니다.


1.7.1 열적 평형 상태
열적 평형 상태는 전자의 존재 확률을 이해하기 위한 기본 개념으로, 진동하는 탁자 위에 쌓인 접시의 예를 들어 설명할 수 있습니다. 탁자가 진동하면 모레도 진동하여 고르게 평탄한 표면이 형성되는데, 이 표면 상태는 외부 선동(agitation)에서부터 최소 에너지 상태로 평형 상태로 정의됩니다.
1.7.2 페르미 레벨
전자가 특정 에너지 상태에 존재할 확률은 페르미-디락 분포를 통해 알 수 있습니다. 페르미-디락 분포의 f(E)는 에너지 상태 E가 전자에 의해 점유될 확률을 나타냅니다. 에너지 E가 충분히 크다면 (E - Ef >> kT, Ef: 페르미 레벨, k: 볼츠만 상수, T: 온도), 그 상태가 전자에 의해 점유될 확률은 E가 증가함에 따라 지수 함수적으로 감소합니다.
간단히 말해, 높은 에너지 대역에는 전자가 적고 낮은 에너지 대역에는 전자가 많습니다. 즉, Conduction Band 위에는 전자가 별로 없고 Valence Band에는 전자가 많다는 의미입니다. f(E)는 전자가 존재할 확률을 나타내며, Ef(페르미 레벨)는 전자가 존재할 확률의 1/2가 되는 에너지 준위입니다.
이러한 이유로 열적 평형 상태에서는 단 하나의 페르미 레벨만 존재하며, 이 개념은 Energy Band Diagram을 그릴 때 매우 중요한 역할을 합니다. 열적 평형 상태가 없으면 모델링에 고려해야 할 사항이 많아지기 때문에 이 개념은 모델링을 간소화하기 위해 도입된 것으로 이해할 수 있습니다.

1.8.1 전자와 정공의 농도
전자의 농도를 구하기 위해서는 전자가 존재할 확률인 Fermi-Dirac 확률 분포와 전자가 존재할 모든 에너지 상태의 수인 Density of State를 곱하고 에너지 범위만큼 적분하면 됩니다. 정공의 농도는 1에서 전자가 존재할 확률을 빼고, 이를 전자와 동일하게 Density of State와 에너지 대역만큼 적분하여 구합니다. 전자는 Ec부터 무한대까지 적분하고, 정공은 가전자 대역 바닥에서부터 Ev까지 적분하면 됩니다.

이렇게 적분하여 얻는 값은 Nc * exp 및 Nv * exp로 나타나며, Nc와 Nv는 유효 상태 밀도 (Effective Density of States)를 나타냅니다. 유효 상태 밀도는 E=Ec일 때의 전자 농도와 E=Ev일 때의 정공 농도를 나타냅니다. Si의 Nc와 Nv는 각각 10^19 cm^-3 정도이며, 유효 질량에 따라 다릅니다.

| Ge | Si | GaAs | |
| Nc [〖cm〗^(-3)] | 1.04 × 10^19 | 2.8 × 10^19 | 4.7 × 10^17 |
| Nv [〖cm〗^(-3)] | 6.0 × 10^18 | 1.04 × 10^19 | 7.0 × 10^18 |
Table1. Effective Density Of States
1.8.2 페르미 준위와 캐리어 농도
전자의 농도가 높아질수록 Fermi Level (Ef)는 Ec에 가까워지며, 정공의 농도가 높아질수록 Ef는 Ev에 가까워집니다. 또한, 온도가 높아질수록 Ef는 진성 Si의 Ef에 가까워집니다. 열적 평형 상태에서는 전자와 정공의 농도의 곱이 일정하며, 이를 np = ni^2 (mass action law)로 나타냅니다.
이 관계는 E-Ef >> kT 조건에서만 성립하며 (Boltzmann Approximation), 불순물이 주입되지 않은 진성 Si에서 생성되는 전자와 정공의 수는 동일합니다. 이를 진성 (Intrinsic) Si라 하며, n = p = ni가 성립합니다. Si의 ni는 약 10^10 개 정도입니다. N 타입 반도체에서는 전자를 Majority Carrier, 정공을 Minority Carrier로 지칭하고, P 타입은 N 타입의 반대 개념입니다.

1.9 n과 p의 일반적 이론
Donor와 Acceptor의 에너지 준위를 각각 Ed와 Ea로 지칭합니다. 일반적으로 Ed는 Fermi Level (Ef) 위에 위치하면 거의 모든 Donor 원자들이 이온화된 상태입니다. Ef는 전자가 존재할 확률을 나타내기 때문에 Ed가 Ef에 위치하면 Donor의 전자들은 대부분 비어있다고 볼 수 있습니다. 이는 Donor 원자의 여분 전자들이 소멸했다고 생각할 수 있습니다.
N type 반도체에 Doping을 하고 Dopant를 거의 이온화시키기 위해서는 이온화 에너지가 Fermi Level보다 높게 위치하면 됩니다. P type은 반대로 Ea가 Ef보다 낮은 에너지 준위를 가집니다 (Valence Band와 가까움).
반도체 내에는 네 가지 종류의 전하를 띤 입자가 존재합니다. 전자(n), 정공(p), Donor 양이온(Nd), Acceptor 음이온(Na)입니다. N type과 P type을 구별하기 위해서는 Nd - Na가 진성 반도체에서의 캐리어 농도 ni (약 10^10 cm^-3) 보다 많으면 N type, 적으면 P type입니다. N type의 경우 Nd가 Na보다 많아야 하며, P type의 경우 Na가 Nd보다 많아야 합니다.
따라서 Donor와 Acceptor 이온의 양을 조절하여 P type에서 N type으로 바꿀 수 있으며, 이를 Dopant Compensation이라고 합니다.
> N type의 경우 다음과 같은 관계가 성립 (Nd >> Na)

> P type의 경우 다음과 같은 관계가 성립 (Na >> Nd)



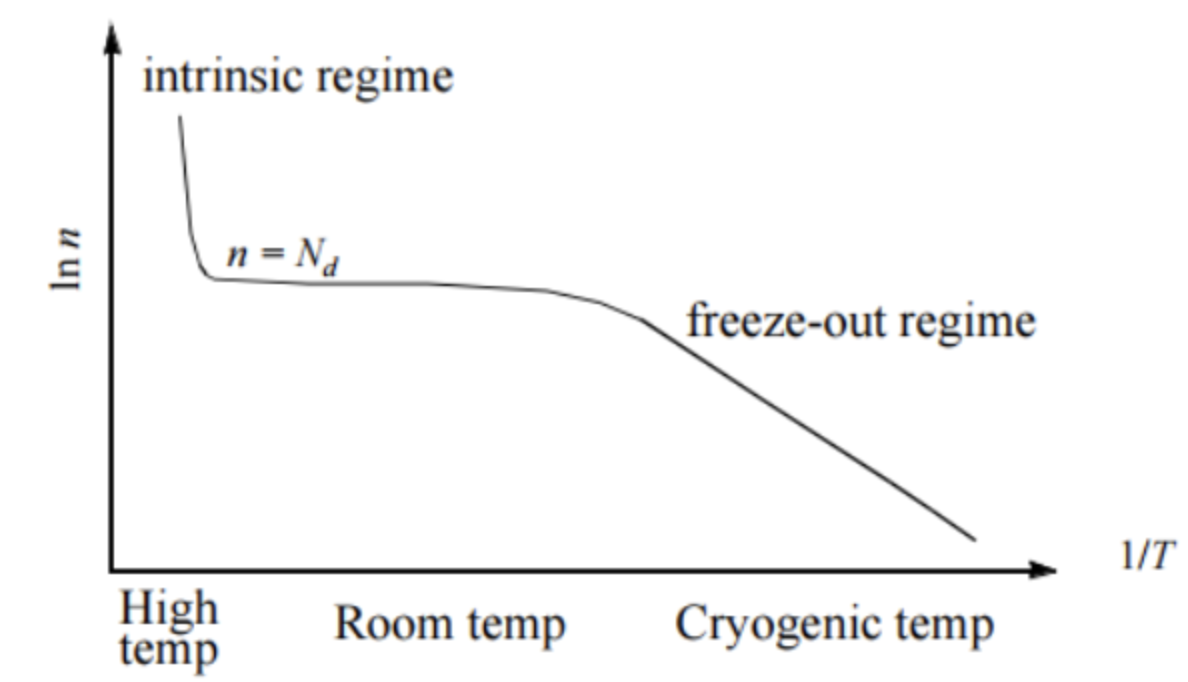
1.10 극고온과 극저온에서의 캐리어 농도
매우 높은 온도에서는 intrinsic carrier 농도 ni가 증가하여 도핑된 캐리어 농도를 능가할 정도가 됩니다. 이러한 상황에서는 도핑에 의한 케리어 농도를 조절할 수 없게 되며, 열 에너지에 의해 생성된 정공과 전자에 의해서만 캐리어 농도가 결정됩니다. 결국 매우 높은 온도에서는 반도체가 도핑되었음에도 불구하고 진성 반도체(Intrinsic)가 됩니다.
반면에 매우 낮은 온도에서는 Fermi Level (Ef)이 Donor의 에너지 준위 (Ed) 보다 높아집니다. 이로 인해 Donor 원자들이 이온화되지 않은 채로 남아있게 됩니다. 도핑에 의한 추가 전자가 Donor 원자에 결합하여 이들은 캐리어 역할을 하지 않습니다. 이러한 상태를 동결(freeze out)이라고 합니다.
'Semiconductor' 카테고리의 다른 글
| 소자 제조 기술 (Device Fabrication Technology) (3) | 2024.06.09 |
|---|---|
| 전자와 정공의 결합 모델(Motion and Recombination of Electrons and Holes) (7) | 2024.06.07 |